2875. Изменение на отрезке (High)

Задан набор из n целых чисел a₀, a₁, ..., a_n-1. Изначально все эти числа равны 0. Далее поступают запросы на изменение и вывод. Для запроса на изменение задаются три числа l, r, d. По этому запросу к каждому из элементов a_i (l ≤ i ≤ r) необходимо прибавить значение d. Для запроса на вывод задается одно число i. По этому запросу требуется вывести текущее значение элемента a_i.

Вход. В первой строке задается два целых числа n и m, обозначающих количество элементов и количество запросов соответственно. В последующих m строках задаются запросы. Запрос на изменение задается строкой вида “A l r d“, запрос на вывод – строкой “Q i“. Все числа целые, 1 ≤ n ≤ 10⁶, 0 ≤ m ≤ 10⁶, 0 ≤ l ≤ r < n, 0 ≤ i < n, |d| ≤ 10³.

Выход. Для каждого запроса на вывод выведите в отдельной строке текущее значение соответствующего элемента.

Пример входа	Пример выхода
10 6 A 3 7 1 Q 4 A 1 5 2 Q 4 Q 1 Q 6	1 3 2 1

РЕШЕНИЕ

структуры данных – дерево Фенвика

Анализ алгоритма

Задачу можно решить при помощи дерева отрезков. Однако из-за ограничения n ≤ 10⁶ решение не пройдет по памяти. Вместо поддержки функции на отрезке (суммы, минимума) в задаче требуется выводить текущее значение одного элемента. Поэтому воспользуемся деревом Фенвика, которое поддерживает две функции:

1. Нахождение суммы на любом отрезке [L; R] за время O(log₂n);

2. Изменение значения любого элемента массива за O(log₂n);

При этом дерево требует O(n) памяти, а именно столько, сколько необходимо для хранения массива из n элементов;

Заведем массив b целых чисел b₀, b₁, ..., b_n-1, изначально равных нулю. При запросе на изменение (поступлении на вход тройки l, r, d, в результате чего следует выполнить операцию a_[l..r] += d) будем делать следующие изменения: b_l увеличим на d, а b_r+1 уменьшим на d. Тогда при запросе на вывод элемент a_i равен сумме b₀ + b₁ + ... + b_i. Например, если l ≤ r < i, то изменения в массиве b при операции a_[l..r] += d никак не повлияют на значение a_i.

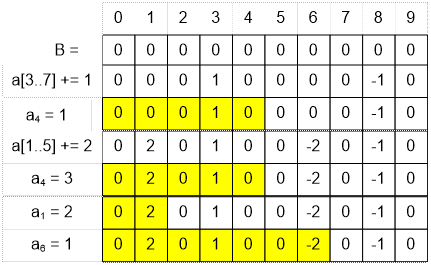
Пример

Промоделируем работу запросов, приведенных в примере.

Реализация алгоритма

Дерево Фенвика храним в массиве Fenwick.

#define MAX 1000001

int Fenwick[MAX];

Функция Summa0_i возвращает сумму элементов b₀ + b₁ + ... + b_i.

int Summa0_i(int i)

{

int result = 0;

for (; i >= 0; i = (i & (i + 1)) - 1)

result += Fenwick[i];

return result;

}

Изменение элемента: b_i = b_i + delta.

void IncElement(int i, int delta)

{

for (; i < n; i = (i | (i+1)))

Fenwick[i] += delta;

}

Основная часть программы. Моделируем выполнение запросов.

scanf("%d %d\n",&n,&m);

for(j = 0; j < m; j++)

{

scanf("%c",&command);

if (command == 'A')

{

scanf("%d %d %d\n",&l,&r,&d);

IncElement(l,d); IncElement(r+1,-d);

} else

{

scanf("%d\n",&i);

printf("%d\n",Summma0_i(i));

}

}

Реализация алгоритма – SQRT декомпозиция – TLE

#include <cstdio>

#include <cmath>

#include <vector>

using namespace std;

vector<int> a, b;

int i, j, n, m, l, r, d, len;

char command;

void update(int l, int r, int d)

{

int i, c_l = l / len, c_r = r / len;

if (c_l == c_r)

for (i = l; i <= r; i++)

a[i] += d;

else

{

for (i = l; i <= (c_l + 1)*len - 1; i++)

a[i] += d;

for (i = c_l + 1; i <= c_r - 1; i++)

b[i] += d;

for (i = c_r * len; i <= r; i++)

a[i] += d;

}

}

int main(void)

{

scanf("%d %d\n", &n, &m);

a.resize(n);

len = sqrt(n) + 1;

b.resize(len);

for (j = 0; j < m; j++)

{

scanf("%c", &command);

if (command == 'A')

{

scanf("%d %d %d\n", &l, &r, &d);

update(l, r, d);

}

else

{

scanf("%d\n", &i);

printf("%d\n", a[i] + b[i / len]);

}

}

return 0;

}